Расшифровка отчета о патологии опухолей молочных желез. диагноз, степень злокачественности. часть 1

Цивилизация или класс?

В социальных науках возникли и развились два основных подхода, претендующих на универсальное объяснение общественной эволюции: классовый и цивилизационный.

Классовый говорит о том, что движущаяся сила истории — классовый интерес и классовые противоречия, именно они создают социальное напряжение, которое выливается в борьбу идеологий и политэкономических моделей. Идеология при этом подходе — концентрированное выражение определённого классового интереса. Либерализм — буржуазии и владельцев капитала, которые стремятся освободиться от чрезмерного контроля со стороны государства и церкви. Социализм — рабочих и пролетариев, требующих освобождения от власти буржуазии и капитала. Национализм — части буржуазии и интеллигенции, которая стремится отгородиться от глобального капитализма и получить власть в рамках конкретного национального государства.

Цивилизационный подход основан на анализе того, как живут, развиваются и умирают различные локальные цивилизации, в чём они похожи и отличны друг от друга. В рамках этого подхода каждая цивилизация порождает собственное мировидение, отражающее идеологию, либо трансформирует в соответствии со своими специфическими особенностями религиозные учения: протестантизм у англосаксов, православие у русских, суннитский ислам у арабов, конфуцианство у китайцев.

Мир-системный анализ предлагает третий подход. Согласно Иммануилу Валлерстайну, в XVI веке в Западной Европе возникает капиталистическая мир-система, охватывающая к XIX веку всю планету. В центре мир-системы находятся технологически развитые страны Запада, Япония и периферия — страны Азии, Африки, Латинской Америки с низкой концентрацией капитала, слабым государством, преобладанием сельского хозяйства и традиционного уклада. Полупериферия (Россия, Китай, Индия, Бразилия, Турция) занимает промежуточное положение.

Русский ответ

Куда бы ни относить Россию и её союзников — к отдельной русско-евразийской цивилизации или к полупериферии капиталистической мир-системы, вызовы, стоящие перед нами, очевидны и очень серьёзны.

С одной стороны, это уже упомянутая архаизация на основе радикальных идеологий. Россия одной из первых столкнулась с исламским терроризмом и практически все последние 25 лет ведёт с ним постоянную борьбу как внутри страны, так и на дальних подступах (Средняя Азия, Ближний Восток).

Радикальный архаизм проник в сердцевину русской цивилизации — на Украину, где сформировался, окреп и получил боевой опыт в форме неонацизма. «Азовское» движение и складывающийся вокруг него «чёрный интернационал» — это русский аналог ИГИЛ, имеющий потенциал распространения не только на Украине, но и в России и Беларуси, Восточной и Западной Европе.

С другой стороны, технологическое отставание от Запада и Китая может стать фатальным и привести к потере субъектности и суверенитета.

Поэтому русский ответ на эти вызовы может быть только комплексным.

Во-первых, обладание теми технологиями, которые могут быть использованы конкурентами против нас в военном смысле или для экономического уничтожения. Как это было с открытием энергии атома. Эту технологию первыми начали осваивать немцы и американцы, которые видели в ней прежде всего военное значение. Американцы первыми использовали ядерное оружие, а русские, тоже получив его, впервые использовали ядерную энергию в мирных целях, запустив АЭС. В этом смысле миссия России — обеспечивать не только собственное выживание, но и направлять развитие технологий на благо всему человечеству.

Во-вторых, архаизирующим идеологиям религиозного фундаментализма и националистического радикализма необходимо отвечать культивированием светского рационального сознания и интернационализма.

В-третьих, в радикально меняющемся, нестабильном мире будущего будет очень большой запрос на безопасность и стабильность, на то, чтобы в водовороте исторических событий кто-то сохранял за собой удерживающую роль или, говоря религиозной терминологией, был Катехоном. У России есть уникальный исторический опыт такой миссии. Россия усмирила и перемолола воинственных степных кочевников, останавливала религиозную экспансию католицизма и ислама, нашествия Наполеона и Гитлера. Сегодня она активно участвует в формировании многополярного мира. И в этом смысле ей не уклониться от реализации в своей внутренней и внешней политике справедливого миропорядка.

Минимизация булевых функций

В данном сервисе для минимизации булевых функций используются метод Квайна и карт Карно-Вейча. После получения минимальной формы имеется возможность заново построить логическую схему. Если исходная схема понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).

Kx v K ≡ K — тождество поглощения;
Kx v Kx ≡ K — тождество склеивания;
Kx v Ky ≡ K(xvy) — дистрибутивный закон,

K_i_ii_i

Метод карт Карно

Склеить можно как целиком всю карту, либо только выделенные единицы (меню Операции). ►

Удалить

Операции

Сохранить как docx
Сохранить как png

Количество переменныхСетка

После минимизации можно получить логическую схему функции и построить таблицу истинности (кнопка Далее)
Далее

Этот метод используется для БФ не более, чем с шестью аргументами и основан на тождестве склеивания: Kx v Kx ≡ K — две элементарные конъюнкции (ЭК) склеиваются, если они отличаются только знаком инверсии одного аргумента. Чтобы облегчить нахождение таких пар (четверок, восьмерок,…) склеивающихся ЭК, используют специальное представление БФ в виде таблицы – карты Карно (другое название — диаграмма Вейча). Чтобы заполнить карту Карно необходимо щелкнуть левой кнопкой мышки на соответствующую ячейку.
Карта Карно обладает той особенностью, что две ПЭК, соответствующие соседним клеткам карты, отличаются знаком инверсии только одного аргумента, т.е. их можно склеивать. Причем соседними являются не только клетки, например, с номерами 1 и 3, но и клетки с номерами 12 и 8, 12 и 4, т.е. карту можно «сворачивать» в цилиндр, соединяя горизонтальные (вертикальные) ее границы.
Две единицы «склеиваются» каждый раз, когда они стоят рядом в строке или столбце (карту можно свернуть в цилиндр). В результате склеивания число букв, входящих в ПЭК, уменьшается на единицу.

Размер опухоли

Размер опухоли чаще всего указывается в сантиметрах или миллиметрах. Этот показатель связан с прогнозом (шансами на выживание) и является частью стадии рака. В большинстве случаев, чем меньше новообразование, тем лучше прогноз.

Маммолог может оценить размер опухоли, почувствовав ее во время физического осмотра. Также для оценки размера опухоли могут быть использованы изображения с УЗИ молочной железы или маммограммы. Однако лучший способ определить размер опухоли – измерить под микроскопом всю опухоль после того, как ее удалили из груди. Патологоанатом запишет данные в отчет о патологии.

Размеры опухоли по стадиям

Сравнение методов решения

Метод рассуждений

Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.

Пример №1.

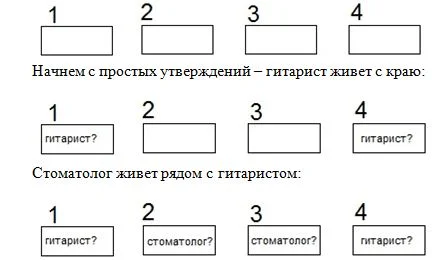
Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.

Известно, что:

дом плотника правее егеря;
стоматолог проживает левее егеря;
дом гитариста с самого краю;
стоматолог живет рядом с гитаристом;
Владимир не гитарист, и его дом не соседствует с гитаристом;
дома Дмитрия и егеря соседние;
здание, в котором прописан Андрей, правее стоматолога;
между домами Андрея и Дмитрия один дом.

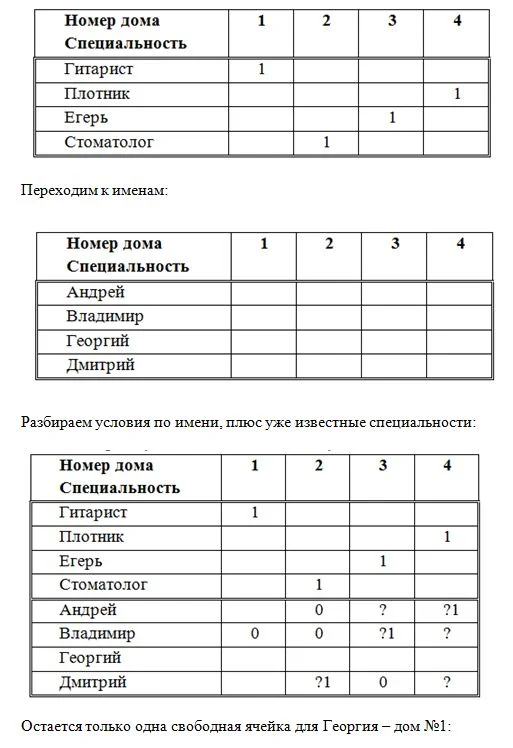
Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:

Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:

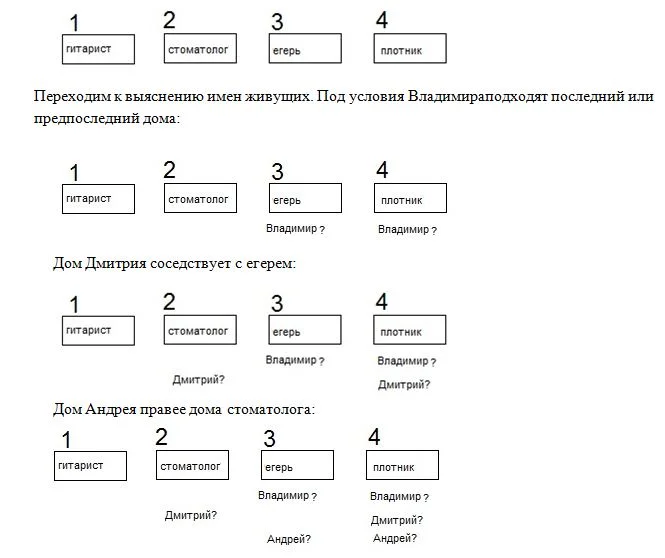
Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.

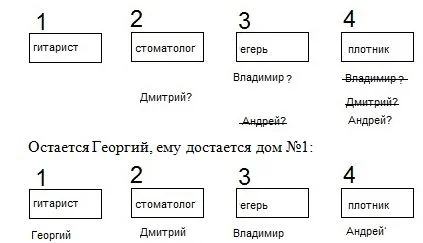
Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.

Такой подход лучше не использовать, если условие сложное или много данных.

Табличный метод

Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).

Чтобы построить таблицу истинности логических выражений, следует:

Разбить задачу на простейшие утверждения, которые обозначить символами (большие буквы латинского алфавита).
Записать условие задачи, как составное выражение из символов логических операций.
Нарисовать таблицу истинности для полученных данных.
Выбрать такой вариант, при котором полученные значения подходят под условие.
Проверить соответствие выбранного варианта и условия задачи.

Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:

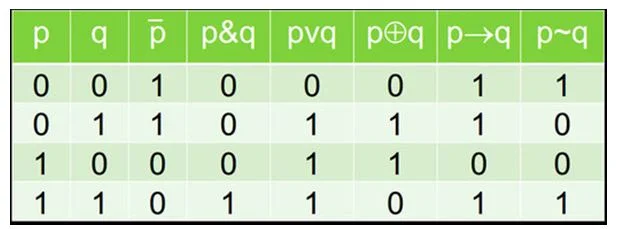
Рассмотрим тот же пример.

Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:

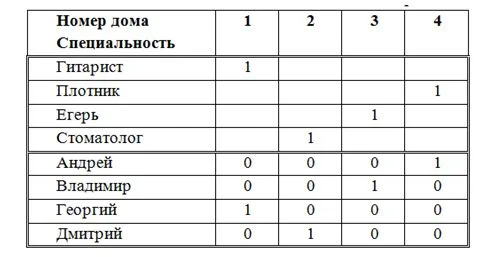
Метод компактнее, для некоторых задач нагляднее.

Технологические вызовы

После 1945 года совместно победившие нацизм идеологии коммунизма и либерализма на длительное время сделали невозможным политическую легитимность расистского, националистического элитаризма. Открытое исповедание расового, национального, религиозного превосходства отдельными личностями, движениями, партиями или государствами фактически было объявлено вне закона. Так было до того времени, пока существовал динамический баланс сил между капиталистической и социалистической системой. Крах последней не привёл к более гармоничному миропорядку, наоборот, масштабировал на всю планету новую идеологическую химеру — мусульманский фундаментализм.

Исламский экстремизм открыл двери для возвращения и распространения от Магриба до Афганистана самой дикой архаики: рабства, геноцида, массового террора. Но это только одна из личин современного Инферно. Технологические открытия в самом сердце цивилизованного мира могут опрокинуть основания его самого.

Генная инженерия. Она открывает возможности «редактирования» человека. То есть потенциально может привести к возникновению колоссального, генетически обусловленного неравенства, когда, например, богатые люди получат возможность «улучшать» себя и своё потомство. И они будут физически и интеллектуально значительно превосходить всех остальных, у кого такой возможности не будет. Это очевидный путь к созданию новых каст и даже рас «избранных» в противоположность «обычным».

Внедрение роботов и искусственного интеллекта в сферу производства будет неизбежно высвобождать большие массы тружеников, лишая их при этом работы и средств к существованию. Чем они будут заняты и не пополнят ли ряды фрустрированных радикалов, готовых на всё? Какая-то часть определённо пополнит, и их будет становиться всё больше.

А это значит, будет расти запрос и на иные идеи. На то, что сдерживает мракобесие и архаику, наполняет гуманистическим содержанием (т. е. не только с целями наживы и господства) любые технологии и научные открытия.

Табличный способ – этапы, особенности

Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.

Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи

Метод таблиц

Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.

Существует общий алгоритм построения таблиц:

Определить число логических значений/переменных (n) в примере.
Установить вид, число и тип операций

Важно заранее определить очередность действий, выразить это при помощи скобок.
Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2n+ 1 (шапка).
Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
Сделать выводы на основании полученных результатов.

Если необходимо перебрать все значения простых выражений, то для задач:

с 2-мя переменными может быть только 4 набора логических переменных;

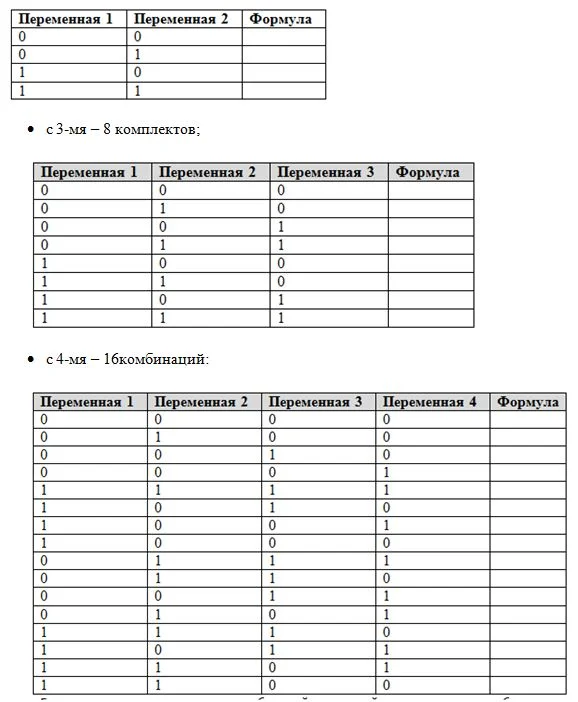
Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.

Обязательно учитывают приоритет операций:

Указанные в скобках.
Отрицание.
Логическая конъюнкция чисел.
Дизъюнкция.
Строгая дизъюнкция.
Импликация.
Эквивалентность.

Способы решения задач по логике

Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:

рассуждая над условием;
решая логические операции;
используя таблицы истинности.

Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.

Этапы решения логических задач:

Разобраться с условием на естественном языке, выделив простые высказывания, и дать им символьные обозначения (латиница).
Записать условие в виде формулы. Решить ее поэтапно, упрощая, учитывая приоритеты (( ), ¬, &, V).
Просчитать формулы строчно или при помощи таблиц истинности, учитывая законы алгебры логики.
Проверить, соответствует ли полученный результат условию задачи.

Построение таблиц истинности для различных типов задач

Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.

Пример 2.

Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.

Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:

А — «Первый студент летал в Англию»;

В — «Второй студент летал в Англию»;

С — «Третий студент летал в Англию».

Запишем выясненные данные при помощи логических операций:

Пример 3.

Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:

Если А получит максимальный бал, то максимальный бал получат Ви С.
А и С получат или не получат максимальный бал одновременно.
Необходимым условием получения высшего бала С класса является получение высшего бала В классом.

По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.

Выясним, какие же классы добились высшего бала.

Разбиваем условие задачи на элементарные высказывания:

А – «А добьется высшего бала»;

В – «В добьется высшего бала»;

С – «С добьется высшего бала».

Запишем логические операции, описанные в примере:

Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.

Пример 4.

Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:

последняя – гласная (Х1);
или первая буква согласная (Х2)
вторая – согласная (Х3).

¬(Х1→Х2)VХ3

Предложенные имена: Арина, Артур, Кэтрин, София.

Решим задачу, используя таблицу.

Сначала решим пошагово, выполняя операции по приоритету:

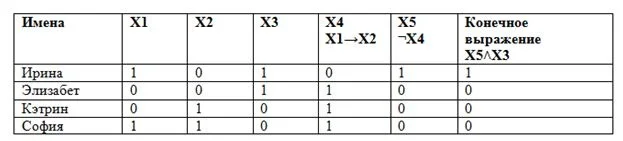
Указанному условию соответствует первое имя.

Пример 5.

Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.

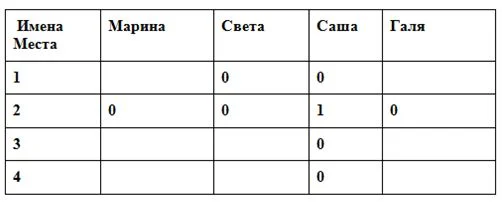
Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.

Маша Марина: «Саша заняла второе место, а Света – первое».

Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».

Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».

Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».

Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».

Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.

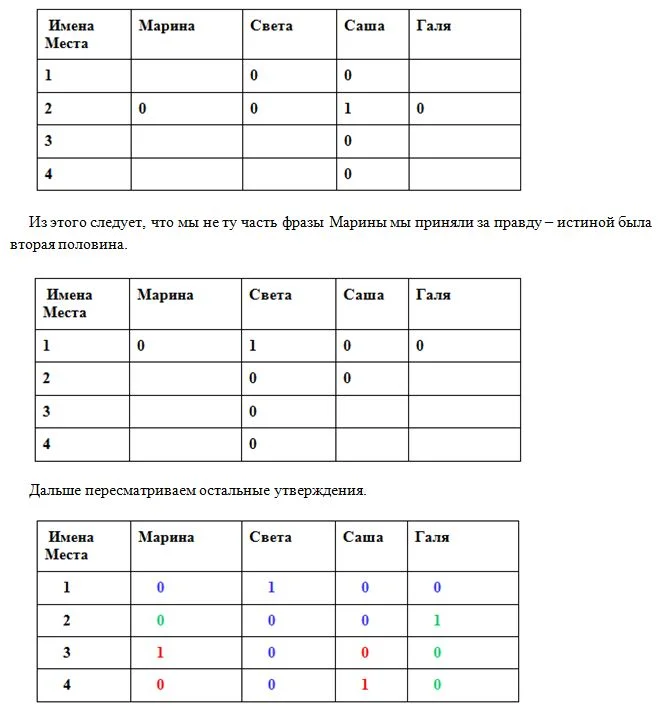
Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.

Число митозов

Число митозов показывает пролиферативную активность образования. Является составной частью общей степени злокачественности и влияет на прогноз патологии.

При определении количества митозов также соблюдают некоторые правила:

подсчитывают в десяти полях зрения;
исследуют периферические участки, так как они наиболее пролиферативны;
в смешанной опухоли частота митозов может быть разная. Если это наблюдается, тогда количество определяют в наиболее митотически активных участках.

Образование составляют тубулярные/канальцевые или железистые структуры	Баллы
> 75%	1
10-75%	2
<10%	3

Ядерный полиморфизм (наиболее анапластическая область)	Баллы
Маленькие, правильные, однородные ядра, однородный хроматин	1
Умеренная вариабельность по размеру и форме, ядра везикулярные с видимыми ядрышками	2
Выраженная вариабельность (явные значительные различия формы и размера), ядра везикулярные, часто с множественными ядрышками	3

Количество митотических фигур в 10 полях. Увеличение 40x или другое (зависит от площади поля, см. ключ ниже). мм2 – единица площади	Баллы
0,096 мм2	0,12 мм2	0,16 мм2	0,27 мм2	0,31 мм2
0-3	0-4	0-5	0-9	0-11	1
4-7	5-8	6-10	10-19	12-22	2
>7	>8	>10	>19	>22	3

Olympus BX50, BX40, BH2, AO или Nikon с окуляром 15x: 0,096 мм2;
АО с окуляром 10x: 0,12 мм2;
Nikon или Olympus с окуляром 10x: 0,16 мм2;
Leitz Ortholux: 0,27 мм2;
Diaplan Leitz: 0.31 мм2.

Сумма вышеперечисленных трех составляющих	Общая оценка злокачественности
3-5 баллов	Степень I (хорошо дифференцированный)
6-7 баллов	Степень II (умеренно дифференцированный)
8-9 баллов	Степень III (плохо дифференцированный)

Построение электронных схем, реализующих логические операции

Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.

Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.

Электросхема с конъюнктором

Рассмотрим все варианты:

Все контакты включены, тогда источник света горит.
Первый контакт в положении «выключено» – свет не горит.
Второй контакт выключен – лампа не светит.
Все контакты отключены – свет не горит.

Заключение – эта электрическая цепь реализует операцию «И».

Дизъюнктор, схема электропитания

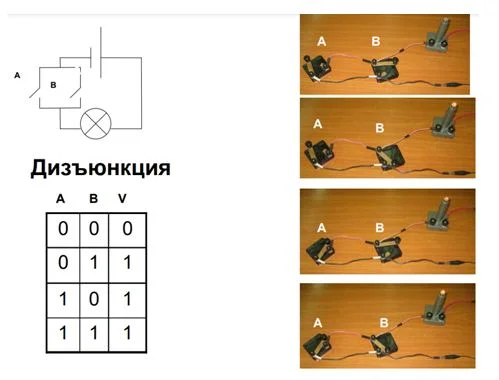
Рассмотрим этот вид электрической цепочки:

Все контакты включены – лампа горит.
Первый контакт включен, второй выключен – свет горит.
Обратная ситуация – выключен первый, включен второй – лампа светится.
Все контакты выключены – света нет.

Заключение – такой вид электросхем соответствует логической операции «ИЛИ».

Инвертор в электросхемах

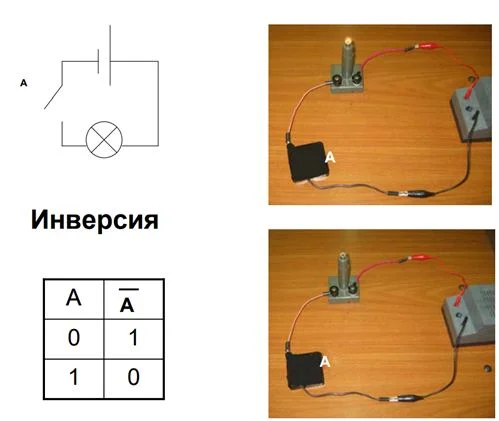
В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.

Заключение: схема соответствует логической операции «НЕ».

Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.

Минимизая функции через равносильные преобразования

Алгоритм минимизии логической функции

Замена импликации и эквиваленции.
Упрощение функции через законы де Моргана.
Раскрытие скобок, используя законы поглощения, исключенного третьего, противоречия.
Минимизация через закон дистрибутивности.

Алгоритм Куайна построения сокращенной ДНФ

Получить СДНФ функции.
Провести все операции неполного склеивания.
Провести все операции поглощения.

Построение логической схемы по таблице истинности

По заданной СДНФ (по таблице истинности) определяются существенные и фиктивные переменные, полином Жегалкина и принадлежность классам T0,T1, S, M, L. ► Также можно создать новую логическую схему (если не выбран пункт Строить новую схему при минимизации булевой функции). Если вычисления происходят по исходной схеме и она понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).

Название переменных можно изменить. Для этого их необходимо выбрать (первая строка таблицы).

Количество переменныхВвести как вектор значений (в виде строки)OK

a	b	c	f

1
1
1	1
1
1	1
1	1
1	1	1

Для установки параметров решения, необходимо нажать Далее.
Далее

Пример. Найдите СДНФ(А) и СКНФ(А) с помощью равносильных преобразований и таблицы истинности, если A = xvyv(x→y)&x

x	y	x	y	xvy	xvy	x→y	(x→y)&x	xvyv(x→y)&x
1	1	1	1
1	1	1	1
1	1	1
1	1	1	1	1	1

xx v yxx v yxxxx_i_i_i_i_i_i_i_i_i_i_i_i_iyxyxyxyxСовершенная дизъюнктивная нормальная форма формулы₁₂_nСовершенная конъюнктивная нормальная форма формулы₁₂_nyx

Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.,1992.
Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс: Часть 2, М.: Мир, 1990.
Горбатов В.А. Основы дискретной математики. – М.: Высш. школа, 1986. – 312 с.

Способы представления булевой функции

С помощью формул можно получать огромное количество разнообразных функций, причём с помощью разных формул можно получить одну и ту же функцию. Иногда бывает весьма полезно узнать, как построить ту или иную функцию, используя лишь небольшой набор заданных операций или используя как можно меньше произвольных операций. Рассмотрим основные способы задания булевых функций:

Совершенная дизъюнктивная нормальная форма (СДНФ)
Совершенная конъюнктивная нормальная форма (СКНФ)
Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Совершенная дизъюнктивная нормальная форма (ДНФ)

Простая конъюнкция — это конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза.Дизъюнктивная нормальная форма (ДНФ) — это дизъюнкция простых конъюнкций.Совершенная дизъюнктивная нормальная форма (СДНФ) — ДНФ относительно некоторого заданного конечного набора переменных, в каждую конъюнкцию которой входят все переменные данного набора.

Например, ДНФ является функция ¬abc ∨ ¬a¬bc ∨ ac, но не является СДНФ, так как в последней конъюнкции отсутствует переменная b.

Совершенная конъюнктивная нормальная форма (КНФ)

Простая дизъюнкция — это дизъюнкция одной или нескольких переменных, или их отрицаний, причём каждая переменная входит в неё не более одного раза.Конъюнктивная нормальная форма (КНФ) — это конъюнкция простых дизъюнкций.Совершенная конъюнктивная нормальная форма (СКНФ) — КНФ относительно некоторого заданного конечного набора переменных, в каждую дизъюнкцию которой входят все переменные данного набора.

Например, КНФ является функция (a ∨ b) ∧ (a ∨ b ∨ c), но не является СДНФ, так как в первой дизъюнкции отсутствует переменная с.

Алгебраическая нормальная форма (АНФ, полином Жегалкина)

Алгебраическая нормальная форма, полином Жегалкина — это форма представления логической функции в виде полинома с коэффициентами вида 0 и 1, в котором в качестве произведения используется операция конъюнкции, а в качестве сложения — исключающее ИЛИ.

Примеры полиномов Жегалкина: 1, a, a⊕b, ab⊕a⊕b⊕1

Алгоритм построения СДНФ для булевой функции

Построить таблицу истинности для функции
Найти все наборы аргументов, на которых функция принимает значение 1
Выписать простые конъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 0, то она входит в конъюнкцию с отрицанием, а иначе без отрицания
Объединить все простые конъюнкции с помощью дизъюнкции

Алгоритм построения СКНФ для булевой функции

Построить таблицу истинности для функции
Найти все наборы аргументов, на которых функция принимает значение 0
Выписать простые дизъюнкции для каждого из наборов по следующему правилу: если в наборе переменная принимает значение 1, то она входит в дизъюнкцию с отрицанием, а иначе без отрицания
Объединить все простые дизъюнкции с помощью конъюнкции

Алгоритм построения полинома Жегалкина булевой функции

Есть несколько методов построения полинома Жегалкина, в данной статье рассмотрим наиболее удобный и простой из всех.

Построить таблицу истинности для функции
Добавить новый столбец к таблице истинности и записать в 1, 3, 5… ячейки значения из тех же строк предыдущего столбца таблицы истинности, а к значениям в строках 2, 4, 6… прибавить по модулю два значения из соответственно 1, 3, 5… строк.
Добавить новый столбец к таблице истинности и переписать в новый столбец значения 1, 2, 5, 6, 9, 10… строк, а к 3, 4, 7, 8, 11, 12… строкам аналогично предыдущему пункту прибавить переписанные значения.
Повторить действия каждый раз увеличивая в два раза количество переносимых и складываемых элементов до тех пор, пока длина не станет равна числу строк таблицы.
Выписать булевы наборы, на которых значение последнего столбца равно единице
Записать вместо единиц в наборах имена переменных, соответствующие набору (для нулевого набора записать единицу) и объединить их с помощью операции исключающего ИЛИ.

Что такое таблица истинности?

Таблица истинности — это таблица, описывающая логическую функцию, а именно отражающую все значения функции при всех возможных значениях её аргументов. Таблица состоит из столбцов и строк, где — число используемых переменных. В первых n столбцах записываются всевозможные значения аргументов (переменных) функции, а в n+1-ом столбце записываются значения функции, которые она принимает на данном наборе аргументов.

Довольно часто встречается вариант таблицы, в которой число столбцов равно n + число используемых логических операций. В такой таблице также первые n столбцов заполнены наборами аргументов, а оставшиеся столбцы заполняются значениями подфункций, входящих в запись функции, что позволяет упростить расчёт конечного значения функции за счёт уже промежуточных вычислений.

Булевы функции

Параметры решения►f(x,y,z) = x → y!zx → y!zУпростить выражение

(...) — ввод скобок, x -отрицание (NOT, !, ¬), & — логическое И, AND, ∧, *, v — логическое ИЛИ, OR, ∨, = — эквивалентность, ˜, ≡, , ⊕ — сумма по модулю 2, | — штрих Шеффера, И-НЕ, AND-NOT, ↓ — стрелка Пирса, ИЛИ-НЕ, OR-NOT, ← — обратная импликация.

(…)
x
˅
&
=
→
⊕
|
↓
←
Clear

Для вложенного отрицания необходимо использовать знак !. Например, x v y = !(x v y) или x v y = x v !y
Далее
Построить схему

По найденной таблице истинности можно определить логические значения высказываний, например, при x=0, y=0, z=1
Чтобы проверить высказывание на истинность или ложность, функцию необходимо вводить без знака равно (=). Например, A+B→A&B=1, необходимо ввести A+B→A&B. Если в результате преобразований получится, что f=1, то высказывание истинно, если f=0 — ложно.

булеву функциюдизъюнкцииконъюнкцииотрицания
Область определения БФ E – конечное множество, поэтому БФ можно задать с помощью таблицы истинности, содержащей |E|=2n строк. Столбец значений БФ при этом представляет собой двоичное слово длиной 2n. Поэтому количество различных БФ n переменных равно 22n.

x f
0 1
1 0
x y f
0 0 0
0 1 0
1 0 0
1 1 1
x y f
0 0 0
0 1 1
1 0 1
1 1 1
x y f
0 0 0
0 1 1
1 0 1
1 1 0
x y f
0 0 1
0 1 0
1 0 0
1 1 0
x y f
0 0 1
0 1 0
1 0 0
1 1 1
x y f
0 0 1
0 1 1
1 0 0
1 1 1
x y f
0 0 1
0 1 1
1 0 1
1 1 0

Основные равносильности логики высказываний

Название	Формула
Закон исключенного третьего	X v !X ≡ И
Закон противоречия	X & !X ≡ Л
Закон коммутативности	X & Y ≡ Y & XX v Y ≡ Y v X
Закон ассоциативности	(X & Y)&Z ≡ X&(Y&Z)(X v Y) v Z ≡ X v (Y v Z)
Закон дистрибутивности	X&(Y v Z) ≡ X&Y v X&ZX v Y&Z ≡ (X v Y)&(X v Z)
Закон двойного отрицания	!!X ≡ X
Закон идемпотентности	X&X ≡ X, X v X ≡ X
Законы де Моргана	!(X v Y) ≡ !X & !Y!(X & Y) ≡ !X v !Y
Закон поглощения	X v X&Y ≡ XX&(X v Y) ≡ X
Законы склеивания	(X & Y)v(X & !Y) ≡ X(X v Y)&(X v !Y) ≡ X
Замена импликации	X → Y ≡ !X v Y
Замена эквиваленции	X = Y ≡ X&Y v !X&!Y

Пример. Упростите выражение: (x˅y˅z)→(x˅y)*(x˅z)
Упростим функцию, используя основные законы логики высказываний.
Замена импликации: A → B = !A v B
Для нашей функции:
(x v y v z)→((x v y) (x v z)) = x v y v z v (x v y) (x v z)
Упростим функцию, используя законы де Моргана: !(A v B) = !A & !B
Для нашей функции:
x v y v z = x y z
По закону дистрибутивности:
(x v y) (x v z) = x v x z v y x v y z
получаем:
f = x y z v x v x z v y x v y z
После элементарных преобразований получаем:
f = x y z v x v x z v y x v y z = x y z v x v y z
f = y z v y z v x

Степень злокачественности опухоли

В случае инвазивного рака молочной железы патолог отмечает форму раковых клеток и присваивает гистологическую оценку, используя систему счисления или слова. То есть проводится градирование только инвазивного (не in situ) образования/компонента.

Степень опухоли описывает структуру клеток и отличается от стадии опухоли. Степень – это способ классификации образований, основанный на определенных особенностях их клеток. Она связана с прогнозом и является частью стадии рака.

В целом, чем больше раковые клетки похожи на нормальные клетки груди, тем ниже оценка и тем лучше прогноз.

Согласно ей опухоли присваивается:

1 степень. Опухолевые клетки больше всего похожи на нормальную ткань и медленно растут (хорошо дифференцируются).
Степень 2. Опухолевые клетки находятся где-то между 1 и 3 степенью (умеренно дифференцированные).
Степень 3. Опухолевые клетки выглядят очень ненормально и быстро растут (плохо дифференцируются).

С помощью микроскопа патологоанатом изучает опухолевую ткань, удаленную во время биопсии, и проверяет ее:

На предмет атипии. Насколько раковые клетки похожи на нормальные клетки (чем больше раковые клетки похожи на нормальные клетки, тем ниже степень опухоли).
На количество митозов. Сколько раковых клеток находится в процессе деления (чем меньше раковых клеток в процессе деления, тем ниже степень опухоли. Это означает, что опухоль также, скорее всего, будет медленно расти).
На ядерный полиморфизм.

Вместе эти факторы определяют степень злокачественности опухоли.

При оценке ткани необходимо соблюдать следующие правила

Препарат должен быть надлежащего качества

- Своевременно и адекватно зафиксирован;
- Исследовать необходимо несколько участков образования, периферической части обязательно (количество участков зависит от размера опухоли, но должно быть не менее четырех);
- Должна быть оптимальная толщина – 4-5 микрон. Если препарат будет слишком толстый, тяжело будет рассмотреть детали.

2. Оценка ядерного полиморфизма и количества митозов проводится в самых “худших”, “ненормальных” участках. Такие участки часто находятся ближе или непосредственно на периферии опухоли.

3. В разных участках (особенно если опухоль смешанная) могут быть разные показатели/характеристики.

4. Всегда и в любом участке образования оценивается состояние железистых структур.